
Steekproef berekenen
Een steekproef berekenen kan lastig zijn. Er moet rekening worden gehouden met verschillende aspecten en verschillende gegevens moeten beschikbaar zijn. Wij nemen u mee in het berekenen van een steekproef. Daarnaast kunt u ook gebruik maken van de steekproefcalculator.
Met onze populaire steekproefcalculator kunt u eenvoudig de steekproefgrootte voor uw onderzoek bepalen.

Een steekproef representeert de populatie. Dit betekent dat hoe groter een populatie wordt, hoe groter de steekproef wordt. Een te kleine steekproef representeert of vertegenwoordigt de populatie niet goed, waardoor er een mogelijkheid ontstaat dat de betrouwbaarheid van het onderzoek niet genoeg toereikend is.

Wanneer een steekproef in verhouding met de populatie te groot is, zorgt dit ook voor problemen. Bij een grote steekproef moeten er namelijk meer enquêtes worden verspreid en meer enquêtes worden geanalyseerd. Dit kan ervoor zorgen dat de kosten (te) hoog oplopen.
De populatie is de groep mensen die wordt onderzocht. De populatie is de doelgroep van het onderzoek. Omdat een populatie erg groot kan zijn (bijvoorbeeld: alle inwoners van Nederland), wordt er een steekproef genomen.
Er is een kans dat de populatie niet bekend is. In dit geval kan er worden gerekend met de oneindige steekproef formule, of kan er bij de calculator een populatie van 20.000 mensen worden ingevoerd. Wanneer een populatie namelijk groter is dan 20.000 mensen, verandert de grootte van de steekproef weinig of niet meer.
Het is belangrijk dat een doelgroep of populatie dus goed wordt gerepresenteerd. Binnen de steekproef moeten alle verschillende bevolkingsgroepen, die zich ook in de populatie bevinden, worden gerepresenteerd.
Wanneer een steekproef representatief is, stijgt de betrouwbaarheid van de doelgroep.
Het is belangrijk dat een onderzoek betrouwbaar is. Op basis van de beschikbare factoren, kan een organisatie zelf bepalen welk betrouwbaarheidspercentage wordt gehanteerd tijdens het onderzoek. Er wordt gewerkt met drie verschillende betrouwbaarheidspercentages, namelijk: 90%, 95% en 99%. Over het algemeen wordt een betrouwbaarheidspercentage van 95% gehanteerd.
Het betrouwbaarheidspercentage heeft te maken met de normaal verdeling. Wanneer men vermoedt dat het grootste deel van de doelgroep tussen de 2,5% en 97,5% valt, wordt er een betrouwbaarheidspercentage van 95% gehanteerd.
Bij ieder onderzoek zijn er afwijkingen in de steekproef. De reden hiervan kan zijn omdat de populatie toch niet voldoende gerepresenteerd is of omdat er niet (volledig) mee willen werken.
Daarom wordt er een nauwkeurigheidsmarge toegepast. Deze marge geeft de mogelijk afwijking weer in het onderzoek. Hoe groter de steekproef, hoe kleiner de nauwkeurigheidsmarge.
De marge is nauwkeurig wanneer er een kans van 50% is dat iemand een antwoord geeft. Dit betekent dat er ook een kans van 50% is dat iemand dat antwoord níet geeft.
Bijvoorbeeld: wanneer er bij een vragenlijst wordt gevraagd naar het geslacht van de respondent, kan de respondent hier ‘man’ of ‘vrouw’ op antwoorden. Een steekproef is nauwkeurig wanneer 50% van de respondenten man antwoord en 50% van de respondenten niet.
In dit geval is de nauwkeurigheidsafwijking 5%. Dit betekent dat wanneer tijdens de vragenlijst 50% van de respondenten aan geeft man te zijn, de werkelijke hoeveelheid mannen bij de populatie tussen de 45% en 55% ligt.
Bij een steekproef berekenen kan er gebruik worden gemaakt van twee verschillende formules. De ene formule wordt gebruikt wanneer de steekproef oneindig is en de andere formule wordt gebruikt wanneer de steekproef eindig is. Wanneer men een steekproef berekenen gaat, moeten de uitkomsten altijd naar boven worden afgerond.
Om de formules uit te kunnen schrijven zijn er bepaalde variabelen, of factoren, nodig. Aan de hand van deze variabelen kan de juiste steekproefgrootte worden berekend. De benodigde variabelen zijn als volgt:
- N N is de populatie. De populatie is de groep mensen die wordt onderzocht.
- z z is de standaardafwijking van het betrouwbaarheidspercentage. De meest voorkomende betrouwbaarheidspercentage is 95%. Hierbij hoort een afwijking van 1,96. Bij een betrouwbaarheid van 90% hoort een afwijking van 1,65 en bij een betrouwbaarheid van 99% hoort een afwijking van 2,57.
- p p is de kans dat iemand een bepaald antwoord wel geeft.
- q q is de kans dat iemand een bepaald antwoord niet geeft.
- F F is de foutmarge. De foutmarge wordt bepaald, door te beslissen welke percentage foutieve enquêtes als acceptabel wordt gezien. Dit kan 3%, 5% of 7% zijn. Vaak wordt er gekozen voor een foutmarge van 5%.
De formule van een eindige steekproef is als volgt:
Voorbeeld: wanneer er een populatie van 10.000 mensen is, wordt er gekozen voor een betrouwbaarheidspercentage van 95%, de nauwkeurigheidsmarge 50% is en de foutmarge 3% is, ziet de formule er als volgt uit:
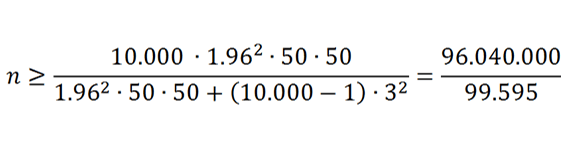
De uitkomst hiervan is 965. De uitkomst is naar boven afgerond, omdat bij een steekproefgrootte berekening er altijd naar boven moet worden afgerond.
De formule van een oneindige steekproef is als volgt:
Voorbeeld: er wordt gekozen voor een betrouwbaarheidspercentage van 95%, de nauwkeurigheidsmarge 50% is en de foutmarge 3% is, ziet de formule er als volgt uit:
.png)
De uitkomst hiervan is 1068. De uitkomst is naar boven afgerond, omdat bij een steekproefgrootte berekening er altijd naar boven moet worden afgerond.
Met onze populaire steekproefcalculator kunt u eenvoudig de steekproefgrootte voor uw onderzoek bepalen.









.png)
















